Nivel:3ESO. Presentamos un proyecto de modelado geométrico tridimensional para dibujar volumetrías de edificios emblemáticos de todo el mundo en baja poligonización, y utilizando figuras geométricas básicas. Aunque el modelado lo realizamos con medidas aproximadas, en el PDF adjunto se pueden consultar las vistas diédricas, en planta, alzado y perfil, para tener una visión global de las proporciones.
Vistas Diédricas
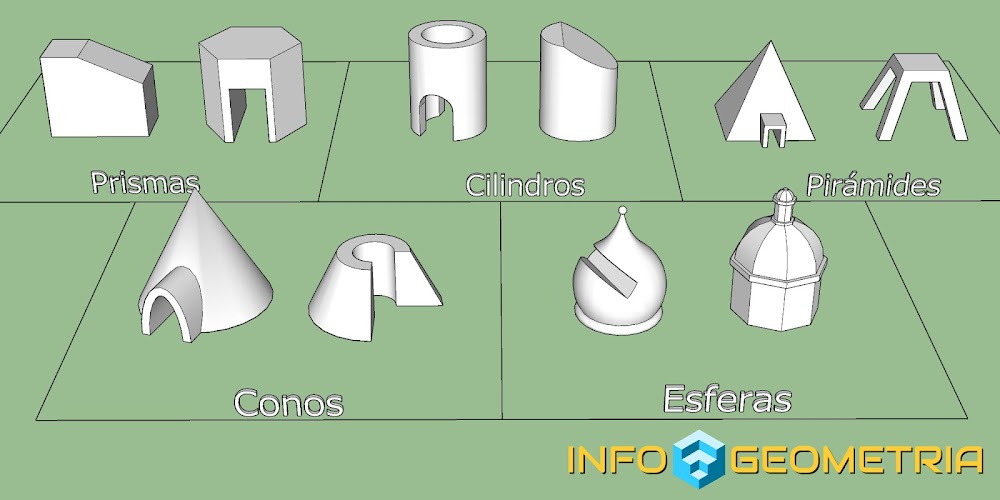
En la siguiente imagen podemos ver en primer plano los cuerpos geométricos básicos estudiados anteriormente. En segundo plano podemos ver las denominadas operaciones Booleanas, un conjunto de operaciones geométricas 3D, con las que podemos obtener cuerpos geométricos más complejos. En el ejemplo, hemos tomado una esfera (A) y un cono (B) para visualizar las tres operaciones básicas. En la primera operación se muestra la unión A+B. En la segunda operación tenemos la posibilidad de sustraer A-B o B-A. En la última de las operaciones Booleanas, se muestra la intersección de los dos cuerpos, A∩B.
1.-Torre Eiffel - Paris.
La estructura básica de la torre Eiffel está generada a partir de tres troncos de pirámide. Observa los tres trapecios rectángulos básicos del perfil, a los que se ha añadido una pequeña moldura y un coronamiento en la parte superior. La revolución del perfil se aplica sobre una trayectoria de base cuadrada. Para finalizar la volumetría se ha sustraído al cuerpo principal dos cilindros y dos prismas, que tienen como base un trapecio isósceles. En la base de los cuatro pilares se ha aplicado una equidistancia para obtener cuatro prismas.
2.-Arco del Triunfo - Paris.
El cuerpo prismático de la estructura básica, se genera a partir de un perfil que revoluciona en una trayectoria rectangular. El cuerpo prismático obtenido, es sustraído mediante dos volúmenes generados a partir de
arcos de medio punto. Para finalizar se ha añadido un pequeño relieve a las paredes con prismas con una pequeña extrusión.
3.-Templo de Kukulcán - México.
El cuerpo de la pirámide se genera mediante un perfil escalonado que revoluciona en una base cuadrada. El trapecio rectángulo, genera un cuerpo prismático con la misma pendiente, dispuesto mediante una matriz polar de cuatro elementos. El coronamiento es un prisma con cuatro huecos pasantes.
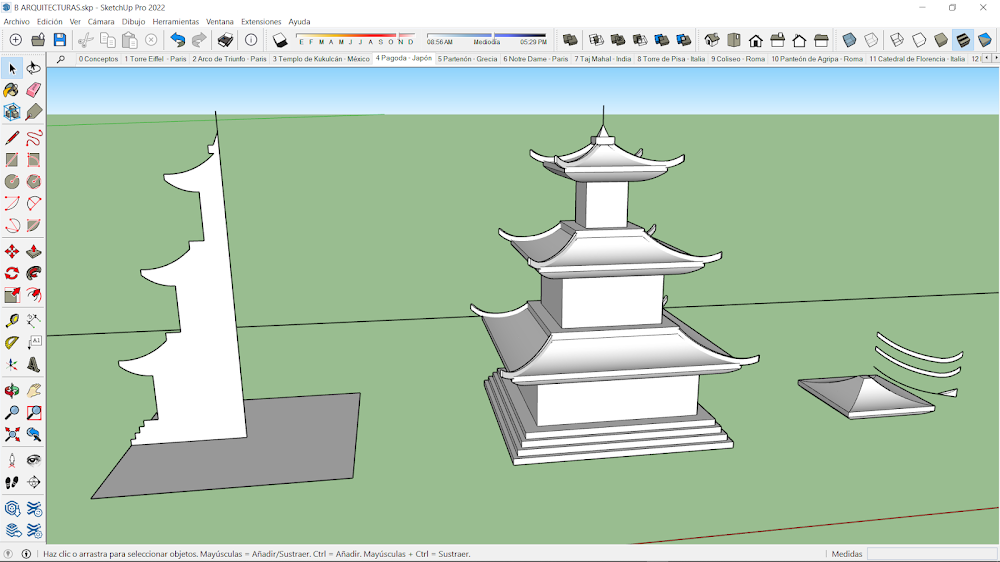
4.-Pagoda Oriental - Japón.
El perfil inicial, se genera mediante segmentos y arcos de circunferencia. Observa que se trata de una estructura modular triplicada, que cuanto más alta, más se acerca al eje de revolución. Los ornamentos de las cubiertas, se generan mediante un perfil extruido, obtenido a partir de una copia de una de las curvas del cuerpo principal. La estructura radial de los ornamentos se consigue con una matriz polar de cuatro elementos.
.png)
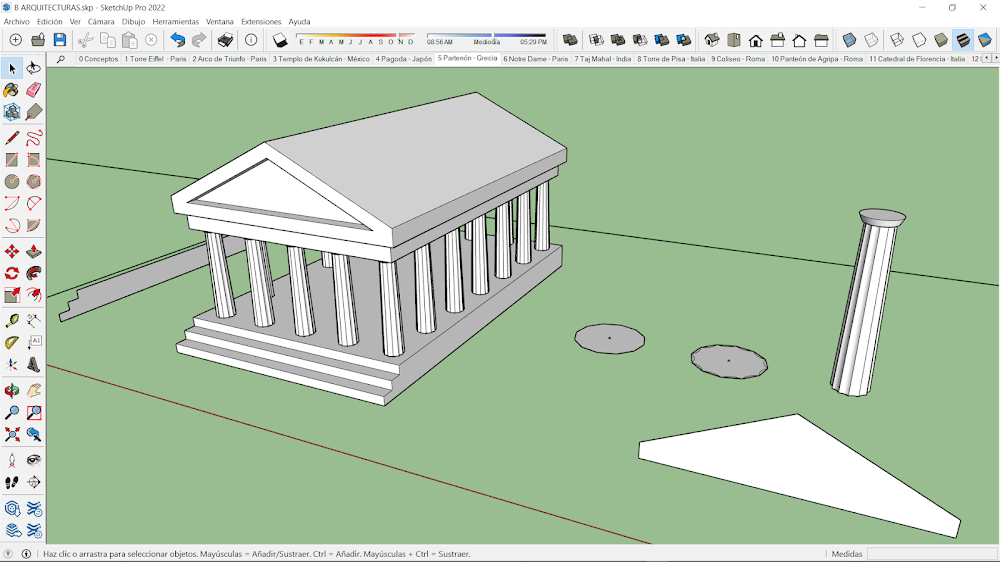
5.-Partenón. Grecia.
La base prismática de la arquitectura, se genera se genera mediante un perfil extruido. Las columnas, con estructura de tronco de cono, se extruyen a partir de un polígono de doce lados modificado. Esta modificación, consiste en añadir una matriz polar de arcos con muy poca curvatura en cada lado. Para representar el capitel, se ha modelado un tronco de cono invertido. Todas las columnas se han multiplicado mediante una matriz rectangular de 5 x 7. La cubierta prismática se obtiene mediante una extrusión de un perfil en forma de triángulo isósceles. La parte del friso se obtiene mediante una equidistancia interior y una extrusión negativa.
.png)
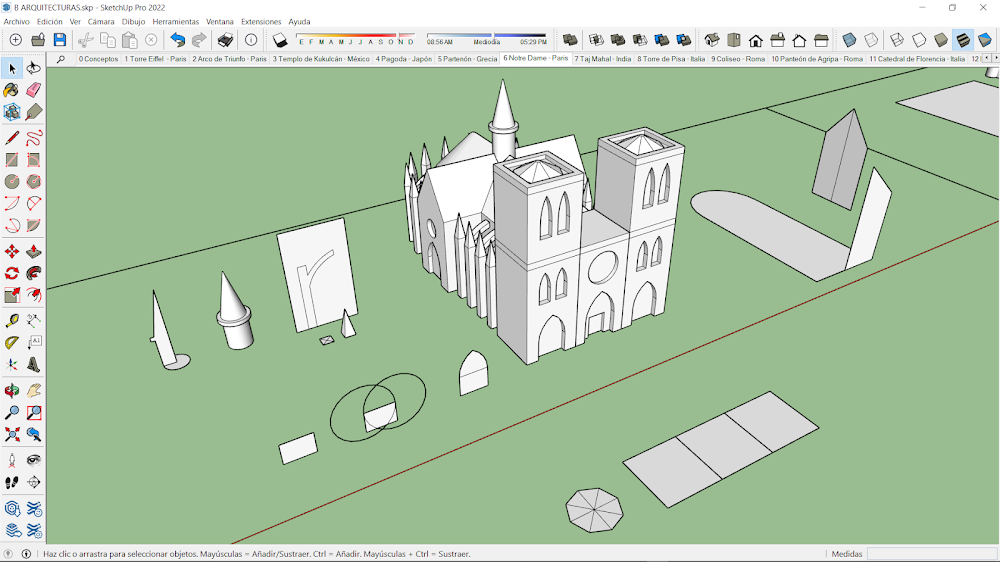
6.-Notre Dame - París.
La volumetría de esta arquitectura presenta muchas figuras. Las torres y la fachada principal son cuerpos prismáticos de base cuadrada, con ventanas y puertas creadas a partir de un mismo componente, en forma de
arco gótico. El rosetón presenta una forma cilíndrica. En la parte superior de las torres se han modelado dos pirámides de base octogonal con muy poca altura. Los contrafuertes y arbotantes se generan mediante un perfil con forma de 'r' y se distribuyen mediante copias rectangulares y polares, alrededor de la nave central y la cabecera respectivamente. La nave central, se genera mediante una revolución de un perfil en forma de trapecio rectángulo, sobre una trayectoria en forma de arco de medio punto. El crucero, utiliza el mismo perfil de trapecio, pero de forma simétrica. el coronamiento de la aguja se representa mediante un cuerpo de revolución formado por dos cilindros y un cono.
.png)
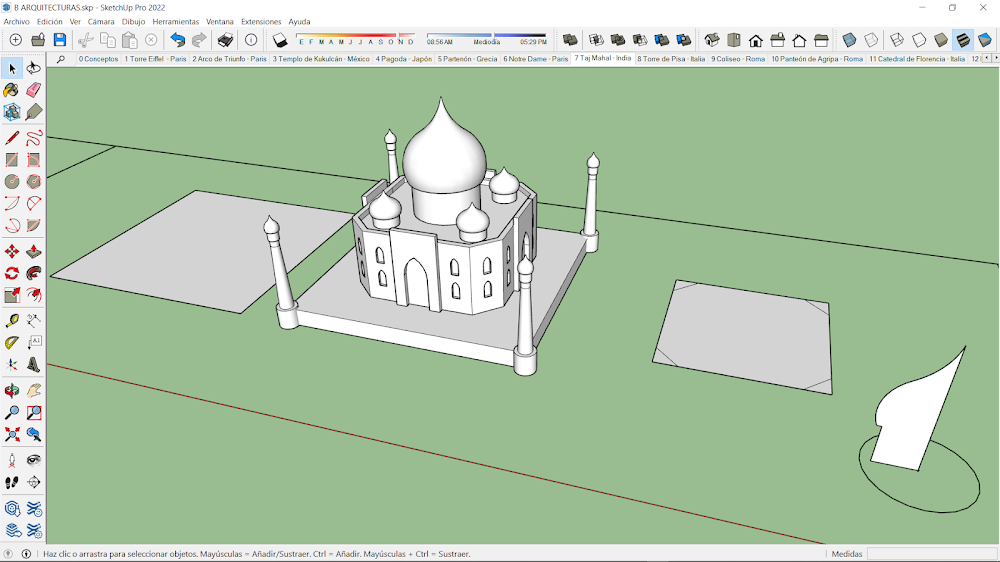
7.-Taj Mahal - India.
La base del templo es un cuadrado de vértices truncados o biselados, que genera un cuerpo central prismático. Las ventanas y portones están generados mediante arcos apuntados u ojivales extruidos de forma negativa. En la parte superior se muestra el tambor cilíndrico y la cúpula bulbosa, generados por una revolución de trayectoria circular. Las cuatro cúpulas menores son copias de la principal a una escala menor. Las torres circundantes, son volúmenes creados con cilindros, troncos de cono y las mismas cúpulas, distribuidos mediante una matriz polar de cuatro elementos.
.png)
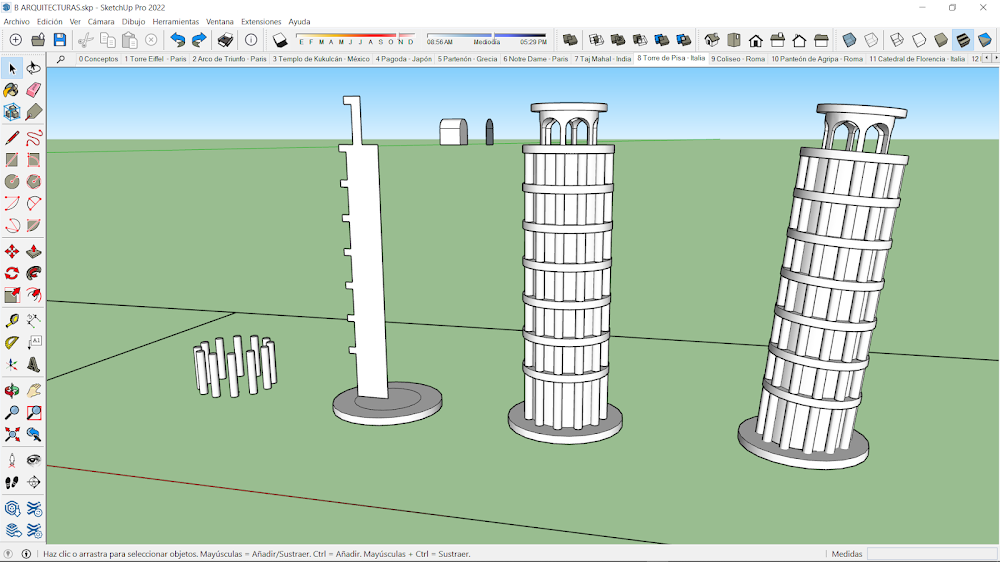
8.-Torre de Pisa - Italia.
El cuerpo de revolución se crea a partir de un perfil rectangular modulado, que gira siguiendo una trayectoria circular. El grupo de columnas cilíndricas se ha generado mediante una matriz polar de doce elementos. Este mismo grupo genera una matriz rectangular en altura para crear el resto de columnas. El coronamiento es un cilindro hueco con una sustracción de seis elementos obtenidos mediante matriz polar. Estos elementos resultan de extruir un arco de medio punto. Al final del modelado la torre se ha girado un pequeño ángulo respecto al eje Z para darle la característica inclinación.
.png)
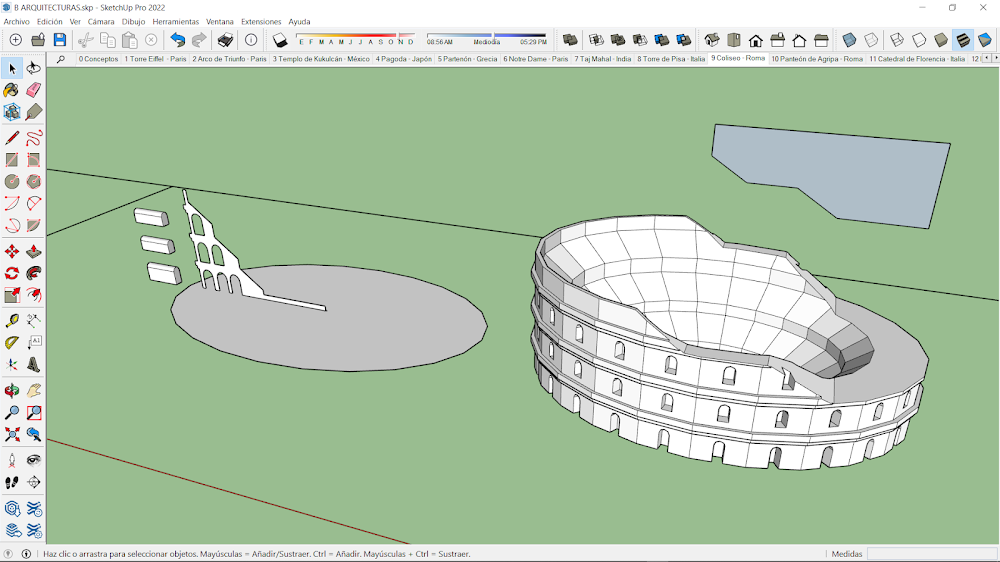
9.-Coliseo - Roma.
El cuerpo de revolución se crea a partir de un perfil compuesto sobre una trayectoria circular. Las ventanas se obtienen con una copia múltiple de 24 elementos mediante matriz polar. Al cuerpo principal se le sustrae todo el conjunto de ventanas. El volumen final se escala en planta para obtener una forma elíptica, que finalmente se sustrae con un un cuerpo prismático, para obtener el característico perfil del monumento.
.png)
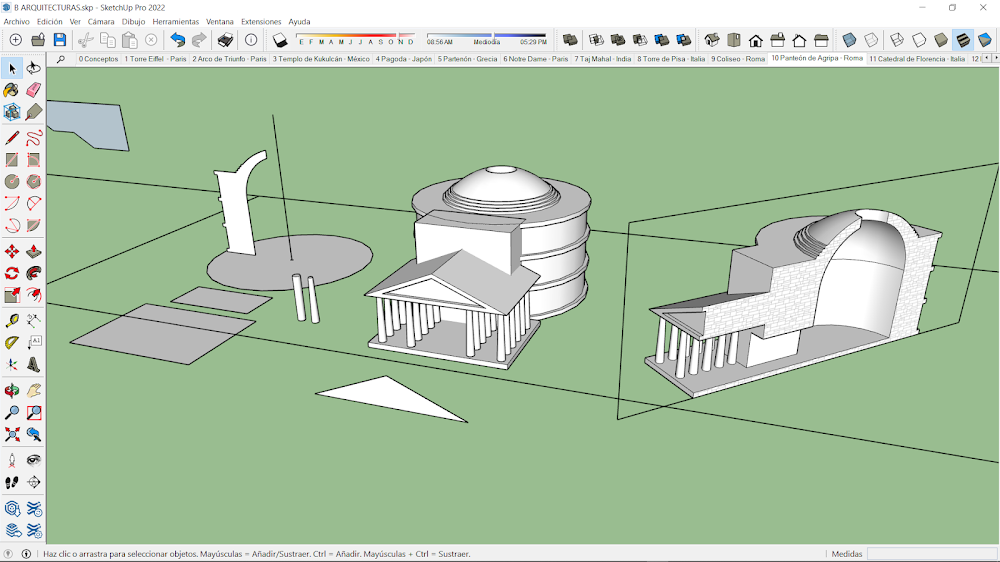
10.-Panteón de Agripa - Roma.
El cuerpo de revolución se crea a partir de un perfil compuesto, que gira siguiendo una trayectoria circular, obteniendo un volumen cilíndrico y esférico. La parte frontal se obtiene mediante la extrusión de varios perfiles rectangulares y triangulares. El friso se obtiene mediante una equidistancia interior y una extrusión negativa. Las columnas representadas como troncos de cono se multiplican según una matriz rectangular. La unión de todos los volúmenes nos da la volumetría general que es seccionada por un plano que pasa por el centro de la arquitectura, eliminando la mitad derecha para representar todo el espacio interior de la bóveda.
.png)
11.-Catedral de Florencia. Italia.
El cuerpo central de la nave es obtenido por una extrusión de un perfil compuesto. La parte frontal de la nave ha sido decorada con puertas y un rosetón. El campanario es un prisma de base cuadrada, con 4 cilindros estilizados rodeando la torre y una pequeña pirámide en lo alto. La cúpula poligonal característica de la arquitectura está generada por revolución, a partir de una trayectoria octogonal. Los prismas y semiesferas laterales, también están generados con una estructura octogonal.
12.-Big Ben. Londres.
El cuerpo prismático y piramidal de la torre está generado por una revolución de trayectoria cuadrada. Los relojes están representados por pequeños cilindros distribuidos de forma radial mediante una matriz polar de cuatro elementos.
13.-Tower Bridge. Londres.
La estructura doblemente simétrica está obtenida fundamentalmente por prismas y pirámides que representan torres y cubiertas respectivamente.
14.-Catedral de San Basilio. Moscú.
Observa la estructura cuadrada de la base, con 4 octógonos distribuidos de forma radial o polar. Toda la volumetría se obtiene mediante cuerpos prismáticos y pirámides. Las cúpulas bulbosas son cuerpos de revolución.















.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)















.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)